HARESH LALVANI 2011-2012

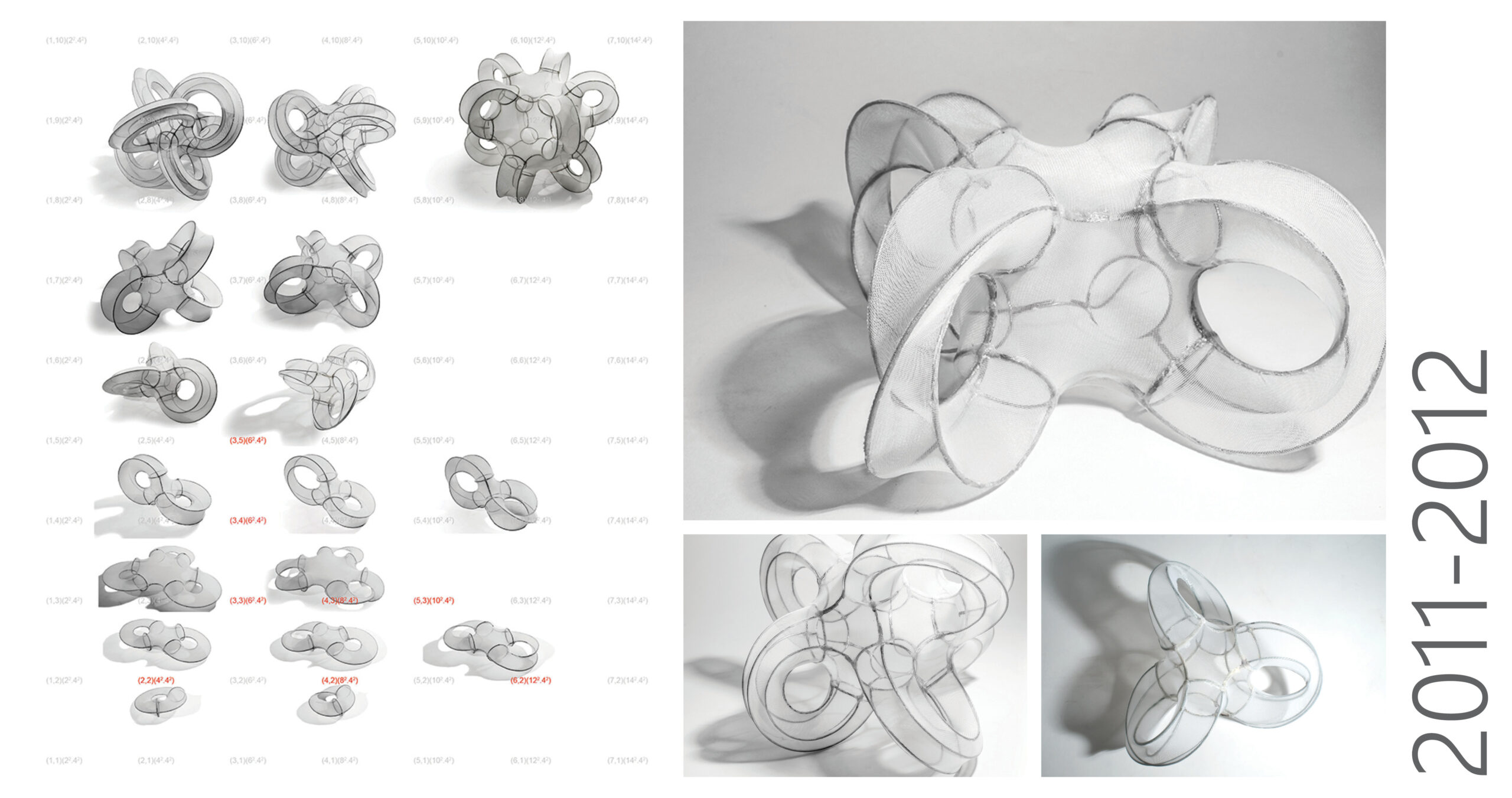
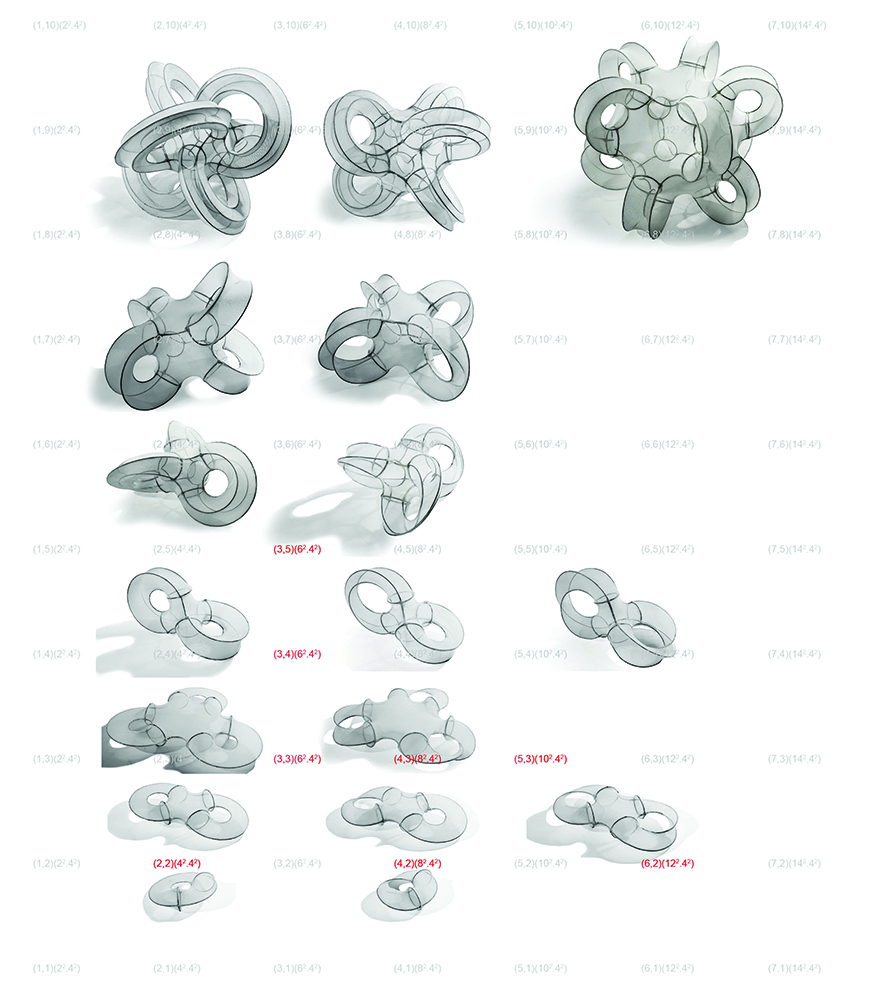
TOPOLOGIES WITH A SINGULARITY

We show portions of our ongoing work in quantum topology for taxonomic generation of infinite classes of minimal surfaces exemplified, in this case, by topologies with a singularity. The physical models shown here are built from wire-frames with stretched membranes, and capture a tiny fragment of the topological universe. The lattice of Schlafli symbols (the superimposed number lattice in the image on the left) is a plane in a higher-dimensional lattice which encodes these topologies. The structures shown are interesting as they exemplify two levels of hierarchy, one dealing with the underlying singularity of space (defined by the first set of numbers in the numeric symbol), and the other defining the surface that shapes space (the second set of numbers). Both, as established earlier in our work, can be morphed continuously to the other, re-iterating our premise that deep structure and surface structure are states of each other. Besides their implication for fundamental structure of physical space, we see their potential as sculptural and architectural spaces and structures.

Prof. Haresh Lalvani, Ph.D.

Physical Models: Wilmer Zamora, Huadong Wang, Justin Hattendorf, Zherui Wang

Graphics: Patrick Donbeck